Section 8 — A Crash Course in Resistance Calculation
You recall that the resistance of a cylindrical wire at a certain temperature is given by:
R = r l /A
Where:
r is the resistivity in W·m
l is the length in meter.
A is the cross sectional area in m2 (pa2 in this case).
The resistance also depends on temperature. A higher temperature, for example, increases the resistance of a copper wire (conductor), while decreases the resistance of a silicon block.
As you may have encountered in your life, conducting materials come in almost every shape and size you can imagine and will not always come in the form of a cylindrical shape. For example, you can see conducting rectangular prisms (bars) in power stations connecting transmission lines and transformers. Conductors may come also in the form of thin sheets. Copper traces in printed circuit boards such as those encountered in computers and other electronic equipments are variations forms of thin conducting sheets.
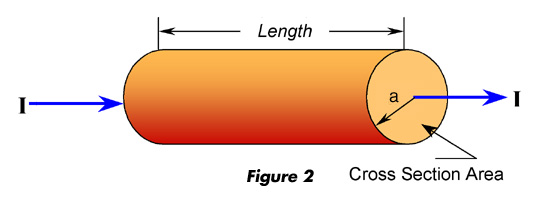
Challenge 15: Consider the copper cylindrical wire shown in Figure 2, if the wire is flattened by a mechanical force (hammer) and made into a rectangular bar but kept same cross section area and length, will its resistance change? Why?
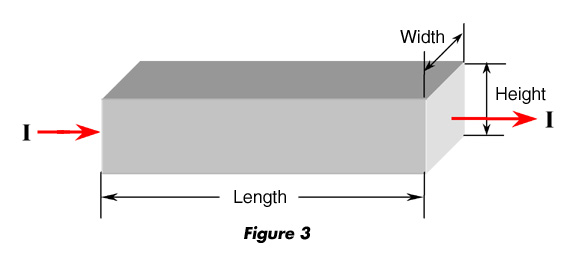
Consider now the silicon block shown in Figure 3, the cross section area in this case is the product of width and height for the current flowing direction shown.
Challenge 16: Does the resistance of this block change if the electric current is reversed? Would the resistance be the same if the current flows from top to bottom? What about from front to back? Explain your findings.
Given that the resistivity of the material is 0.005 W.m at room temperature, find the resistance in each case. Assume a set of values for the length, height, and width.
Let’s also consider the aluminum sheet shown in Figure 4. The current flows in this case from one side of the sheet to the other. The length in this case is the distance between the two copper buses along the current flow.
What would the cross section area in this case be? Think about that for a minute.
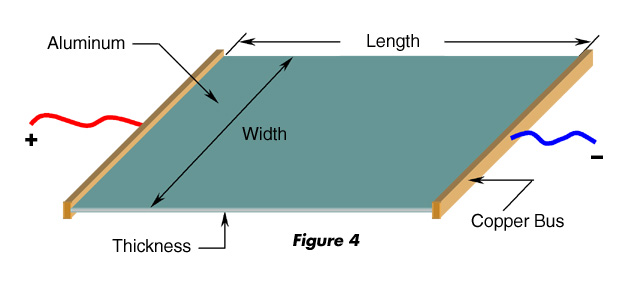
Right, the cross section area in this case is the product of width and thickness.
Challenge 17:
• Assume that the above sheet is made of PolythermTM with resistivity of 0.035 W.m at room temperature. Let the length, width, and thickness be 0.1x0.03x0.0004 m, can you find the resistance if the current is flowing from left to right?
• What is the resistance of the sheet if the current is flowing from top to bottom? How about from front to back?
• Did you get the same value? Explain why!
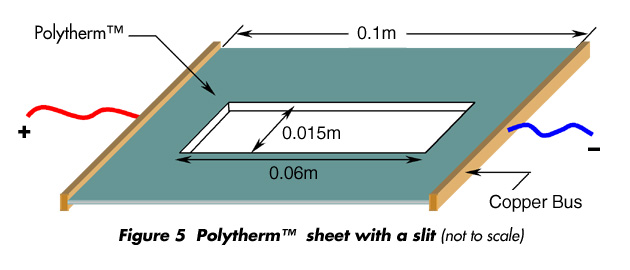
Now, let’s make it a little more challenging this time! Let’s cut a rectangular slit (hole) in the above PolythermTM sheet in a similar way to the one shown in Figure 5. Examine the resistance again assuming same dimensions (0.1x0.03x0.004) and current flow.
Challenge 18:
• Does the resistance change by introducing the slit? How?
• Does the location of the slit change the resistance of the sheet? Why?
• Let the slit length and width be 0.06x0.015, can you find the resistance if the current is flowing from left to right?
• In comparing the two cases with and without a slit, does the resistance of the sheet change assuming a current flow from top to bottom? How about from front to back? Explain why!



